Octahedron unit-vector encoding

There are many situations in Computer Graphics where you may need to store massive amounts of unit-length vectors (e.g., directions, surface normals, …). The normals AOV in a G-Buffer, incoming directions in a Photon map, or uploading a 3D model to the GPU for rendering are situations that greatly benefit from a bit-efficient encoding for normals.

Spherical coordinates encoding

The straightforward way to encode a normal is to store its (x,y,z) coordinates, which takes 3x32=96 bits in single-precision floating-point. This naive approach doesn’t take advantage of the fact that in normals or directions the vector length is irrelevant. So assuming unit length, you may use spherical coordinates (theta, phi) and encode each normal with 2 numbers instead of 3.

Since (theta, phi) have a [0..2pi] and [0..pi] range, it sounds reasonable to quantize its values using fixed-point math. This way both angles become a couple of integers of, say, 16-bit each, with their ranges turned into [0..65535]. Note that this gives twice as much resolution to phi but that’s fine. We have achieved a reasonably fine-grained 16+16=32-bit encoding. Depending on how tolerable precision losses are in your application, you may go even lower (e.g., 12+12=24-bit, or even 8+8=16-bit).

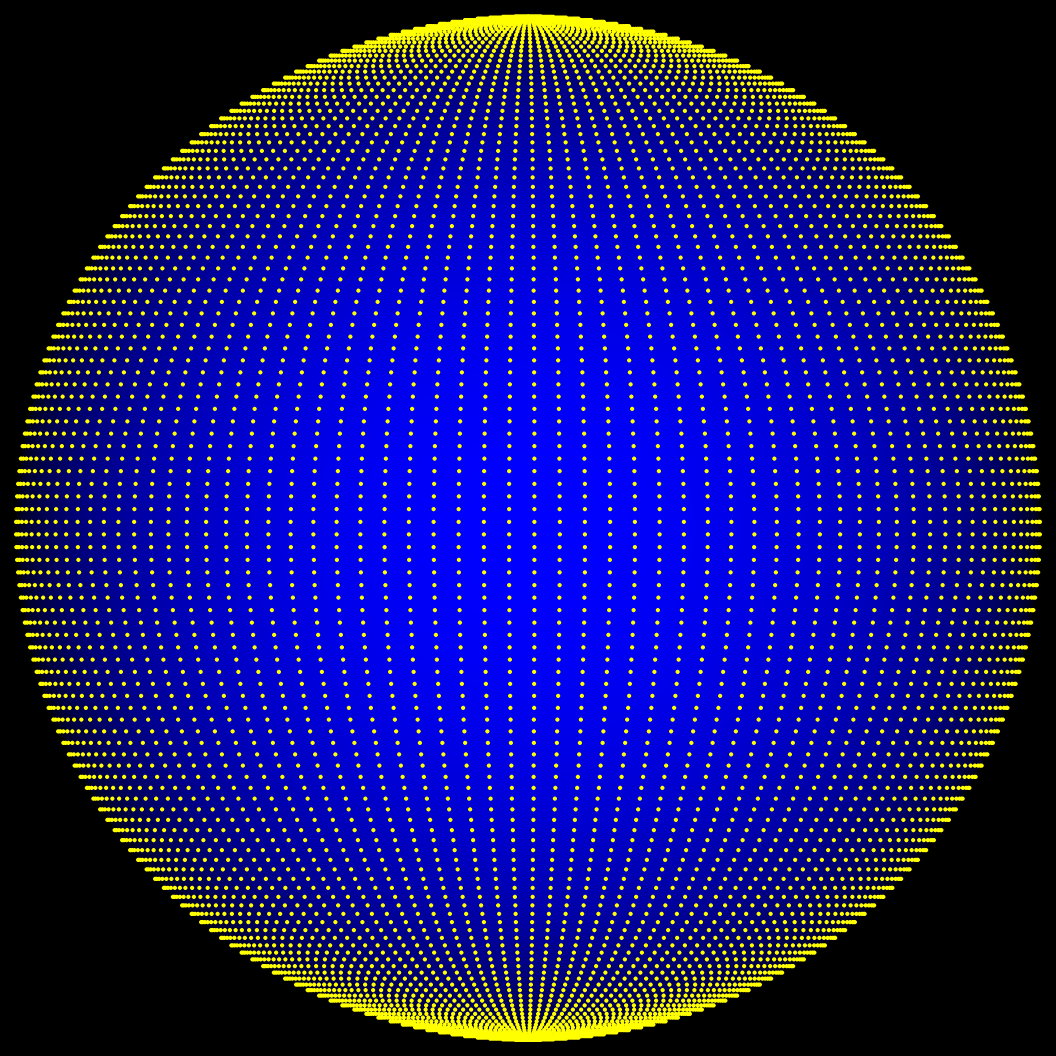
The problem with this simple approach is that spherical coordinates are not an equal-area transform, as they concentrate points near the poles.

Spherical coordinates encoding: phi gets more precision than theta, and density between the equator/poles is highly uneven.

Octahedron encoding

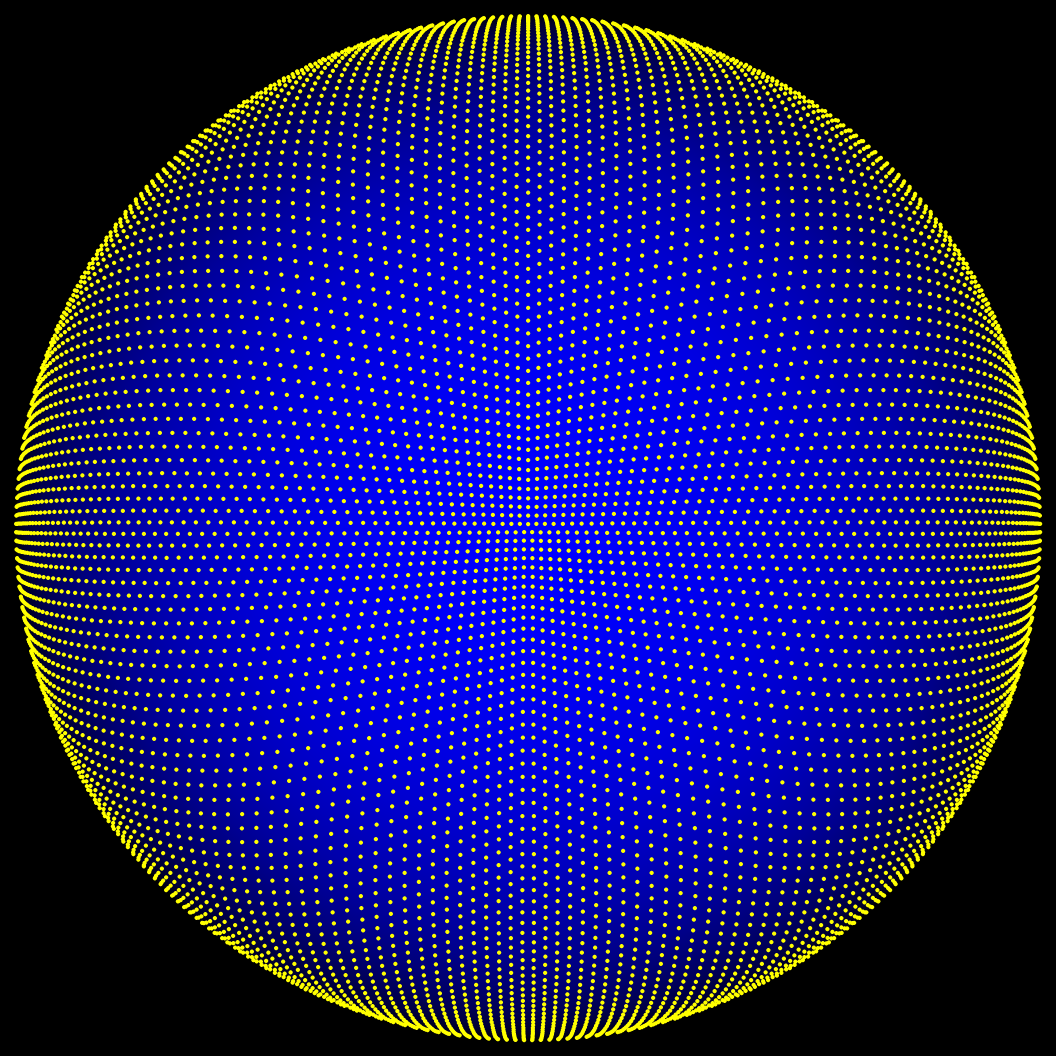
A smarter solution which produces a much more even distribution, while being strikingly simple and more efficient computationally (no trigonometry whatsoever) is octahedron encoding.

Octahedron encoding: The distribution is pretty even.

The idea is to project positions in the sphere (unit vectors) onto a sphere-centered octahedron. And then piece together the 8 faces of the octahedron in the unit cube. This diagram should be self-explanatory.

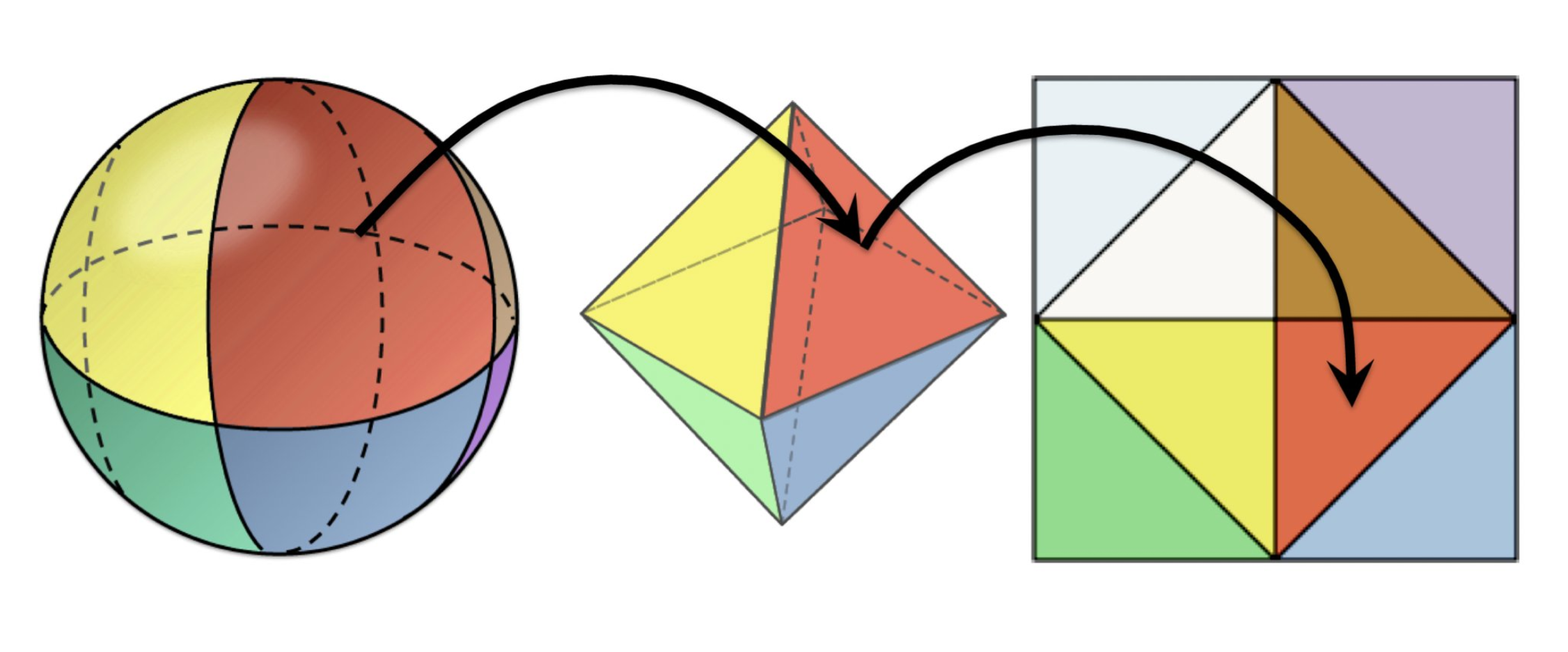
Reference: Octahedron environment maps

Fibonacci encoding

Recently I have been using the Fibonacci lattice here and there and had the idea to use its equal-area spherical flavor for normal encoding. After googling a bit I came across this paper, so somebody had the idea first:

Unorganized Unit Vectors Sets Quantization

Actually, pulling from this thread I also came across these Shadertoy samples by Íñigo Quilez. They visualize what happens with either method as more bits are budgeted for normals encoding:

Fibonacci: Shadertoy #1

Octahedron: Shadertoy #2

Fibonacci encoding: Looks great, but comes at a price.

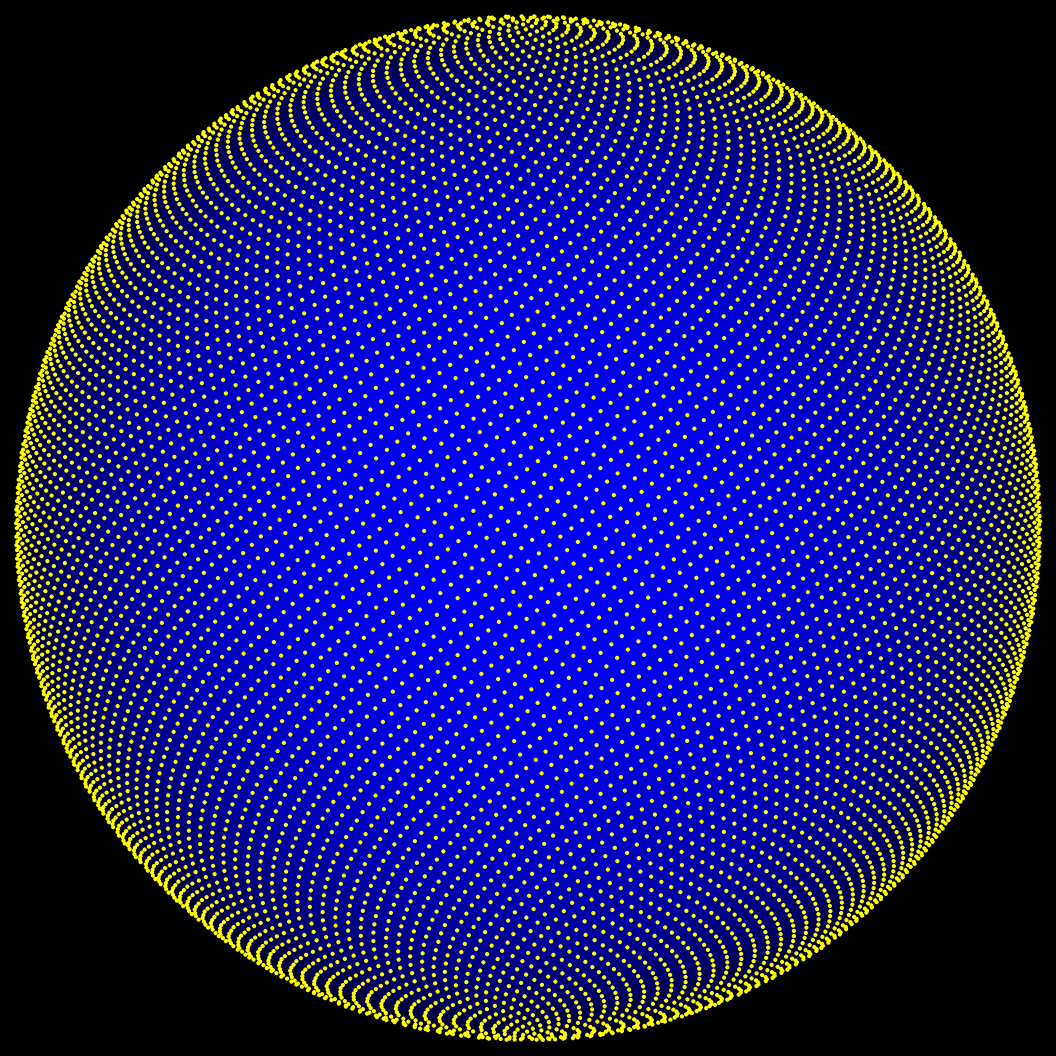
This looks elegant (pretty even!). Unfortunately the implementation to encode/decode unit-vectors with n bits is rather convoluted and involves N=2^n and 1/N. As soon as n>24 or so numerical degradation makes this solution unusable in single-precision. Also, this method is significantly slower than octahedron encoding, and while the distribution looks prettier, the difference in practice is negligible.